Overview
In this resource, we discuss the teaching and learning of addition and subtraction. Often, students’ understanding of this topic is heavily grounded in rote computation of numbers, separated from any real-life context. Unfortunately, this can leave gaps in their understanding of the concepts that underlie those computations. This resource shows how the use of context—story problems—can help students develop a real grasp of addition and subtraction.
Key Concepts
Modeling
A story problem introduces addition and subtraction not as a mathematical procedure, but as a hypothetical real-life problem in context. The student then must take the conceptual leap of turning the real-life problem into a mathematical problem—providing some of their earliest experiences with the important mathematical practice of “modeling.”
Story Situations
There are several different kinds of mathematical relationships that students must infer from story problems. These are known as “situation types.” The Common Core State Standards (CCSS) expects K-1 students to understand four situation types:
- Add-to
- Take-from
- Put-together/take-apart
- Compare
Teachers who understand the situation types (and what is new and challenging about each one) are better able to select and sequence problems that help students build their conceptual understanding of addition and subtraction.
Building Conceptual Understanding of Addition and Subtraction
The ability to add and subtract are widely recognized to be fundamental mathematical skills. However, we do not always recognize the other important conceptual understandings that students gain through solving story problems, beyond the computational skills gained by practicing addition and subtraction facts without context.
The following diagram from the Program for International Student Assessment (PISA) outlines the steps students go through when solving problems with real-world contexts, and may point to what we want to build in students as they are introduced to addition and subtraction story problems.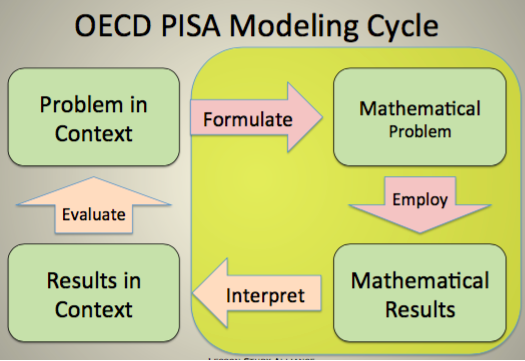
Addition and subtraction story problems are some of the first experiences students will have using the important mathematical practice of modeling. Let’s take a look at an example problem to see what this process might look like for Kindergarteners.
In this problem, we start with the problem in context: we see that there are 5 fish in a tank, and a child is adding 3 more. Next, students must represent this situation mathematically. This can be done with manipulatives (as is shown with the yellow blocks below) and by using the number sentence, 5 + 3 = ?. Students who are newer to solving story problems will rely on the more concrete representation of manipulatives.
As students build fluency of composing and decomposing numbers (and familiarity with story problems), they can jump to representing the problem with a number sentence.
Once students solve the mathematical problem to discover the answer is 8, students must return to the context of the problem and interpret the results. In this case, 8 refers to the total number of fish in the tank.
Story Situations
As we mentioned previously, students develop their understanding of the addition and subtraction operations as they use them to solve story problems. There are several categories of story problems, known as situation types, that describe the relationship among quantities in story problems. The four situation types that the Common Core State Standards (CCSS) require students to learn in grades K-1 are:
- Add-to
- Take-from
- Put-together/take-apart
- Compare
Teachers who understand the situation types (and what is new and challenging about them) are better able to support their students in developing a strong conceptual understanding of addition and subtraction. For this reason, we want to spend the rest of this resource familiarizing you with the four addition and subtraction story situations.
The Addition and Subtraction Story Situations
To get a better idea of what we mean by “situation type,” let’s return to our example addition problem, which represents an add-to situation. In this problem, one quantity (3 fish) is added to an existing quantity (5 fish), resulting in a new quantity (what we discover to be 8 fish). The details of the problem can change (for example, it could involve cookies instead of fish) as can the unknown quantity (for example, perhaps we knew how many fish we had in the end, but not how many we started with), but the relationship among quantities is the same for all add-to problems.
Below, we represent the add-to situation as a diagram, and label each quantity as the CCSS refers to them (start is increased by change to become result). We don’t recommend introducing the diagram as a model to students, but it be may be helpful as teachers to see the situation type represented visually.
Another important thing to understand is that the situation type itself isn’t how we know whether to use addition or subtraction. Rather, we determine the needed operation based on which quantity is unknown. In our example above, 3 fish are being added to an aquarium of 5 fish, and the unknown is the total number of fish (5 + 3 = ?)—so this requires addition. But if we added 3 fish to a tank that now has 8 fish, this is still an “add-to” situation: ? + 3 = 8), but we would use subtraction to find the unknown (8 – 3 = ?).
In the table below, we provide an example problem for each type of story situation and a diagram that represents each situation’s relationship among quantities.
Discussion Questions
After reading this resource, it may be helpful to discuss the following questions as a team.
- What ideas about the teaching-learning of addition and subtraction discussed in this resource strike you as important in your setting?
- How does your curriculum handle addition and subtraction story problems? Which situations does it introduce first? What about it do you like and/or notice that has opportunity for improvement?
- What experiences have your students had that currently inform their understandings of addition and subtraction?
- How do your students represent story problems?
- What do you want to learn more about and what steps can you take to do so?
Next Steps
In our resources linked below, we take a closer look at the situations, and discuss what situations (and which unknown quantities within situations) are challenging for students and how to support them to overcome the difficulties.
First, we take a close look at the situation types that students typically first experience: add-to, take-from, and put-together/take-apart.
Second, we discuss the compare situation.
Finally, we return to add-to and take-from situations to cover how students solve for unknown start or change values.
