Lesson Study works best with rich subject content. This course offers step-by-step support to conduct a Lesson Study cycle on fractions, by providing fractions resources and research to examine.

Examine Grade 4 Curriculum Materials
To see how the grade 3 unit lays the foundation for understanding equivalence in grade 4, we suggest that your team goes on to:
Read the grade 4 fractions unit titled Mathematics 4B for Elementary School, noting any tasks or experiences that build student understanding around the key fractions challenges. Use the Worksheet: Tasks and Experiences that Build Fraction Number Sense to record your thinking. Both resources appear in the tiles below.
If time permits, look over the translated segments of the 3B Teacher’s Edition and 4B Teacher’s Edition for additional insight into how the grade 3 and 4 textbook units build student understanding around key fractions challenges.
Discuss any new thoughts group members have written on the Tasks and Experiences that Build Fraction Number Sense worksheet and any new insights about the following questions:
- How do these textbook units build an understanding of equivalent fractions? How are students helped to see that the same point on the number line can be described with different fractions (and sometimes mixed numbers)?
- How do these textbook units build understanding of multiplication of a fraction by a whole number?
- In the treatment of the above topics, what is similar or different from your curriculum?
Read the Summary of Video Excerpts below.
Watch the video segment below. After watching, discuss:
- Why might it be helpful to use the fraction strips and number line together to build understanding of equivalence? How is this similar or different from how your curriculum builds understanding of equivalence?
- At the end, Dr. T. talks about the importance of students seeing (unit) fractions as new units made by dividing a whole into equal parts—that any unit fraction, say , is made by dividing the whole into “a” equal parts. He also talks about students seeing that these new units can be used to measure other quantities. (For example, meter lengths can be used to measure 1 ) How does your curriculum build these understandings?
Lesson Series 2
If time permits, you may find it valuable to examine a second series of lessons taught by Dr. Takahashi in Illinois. The intent of these lessons was to show how to build upon the grade 3 lessons in order to help students understand equivalent fractions. But Dr. Takahashi discovers that he first needs to help students grasp fractions as equal parts of a partitioned whole and strengthen their knowledge of fraction notation and number line conventions. Dr. Takahashi’s efforts to elicit and support student thinking make for fascinating viewing that will help you think through student thinking that may occur in your setting also.
Take a look at the Lesson Series 2: Summary of Video Excerpts and Dr. Takahashi’s slides for these lessons. If your time is limited, we recommend that you look at the video in the order suggested below (there is no Day 2 video), going as far as your time permits.
Watch Day 1: Connecting Fraction Strips to Number Line (22 minutes); have team members focus on both of the following questions, taking notes on the Video Observation Notes. After viewing, discuss:
- At the outset, no students use the number line to show the problem. What elements of instruction help students see the meaning and usefulness of the number line, and build their comfort using it?
- What challenges in understanding the number line surface in this lesson?
Watch Day 3: Connecting Fraction Strips to Number Line (10 minutes); have team members focus on one of the following questions, taking notes using Video Observation Notes. After viewing, discuss:
- What is difficult about mixed numbers for these students and why?
- How does Dr. Takahashi help students connect fraction strips, the number line, and fraction notation?
Watch Day 4: Connecting Fraction Strips to Number Line (22 minutes); have team members consider the following three questions, taking notes on Video Observation Notes. After viewing, discuss:
- What specific misunderstandings of fractions surface during this lesson?
- What understandings does the lesson seek to develop?
- What elements of instruction support students to progress in their understanding?
Linear Measurement in the Early Grades: A Foundation for Fractions
As you consider fractions in a linear measurement context, you may also find it interesting to think about length and measurement activities that lay the groundwork in earlier grades. In the Japanese grade 1 curriculum, students measure common objects using different units; for example, they might measure their desks using pencil lengths and eraser lengths. They also compare the length of different objects placed on a grid, as shown in below.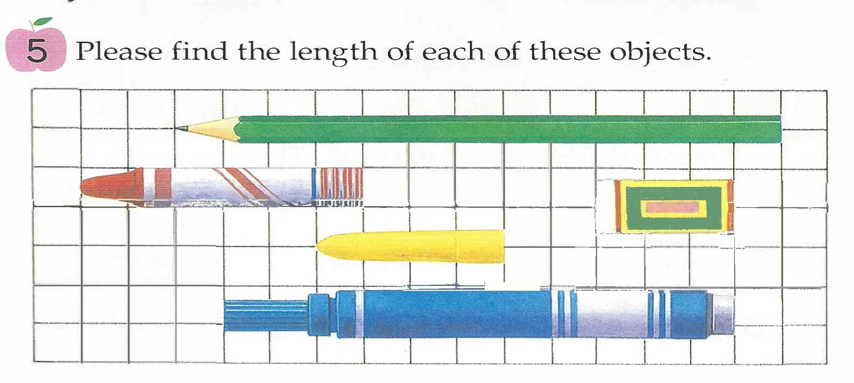
If time permits, your group might want to discuss the following two issues:
- What understandings do students develop from using two different objects (such as a pencil and an eraser) to measure the length of their desk? How might such understandings support later understanding of fractions?
- Why are the objects on the grid arranged as they are? Why might the grid itself be useful? What knowledge from this task might support students’ later understanding of fractions and number lines?


