Lesson Study works best with rich subject content. This course offers step-by-step support to conduct a Lesson Study cycle on fractions, by providing fractions resources and research to examine.

Models of Fractions
Researcher: Which fraction is smaller, 6/4 or 6/5?
Chris: 6/4. Because 4 takes longer to get to 6 than 5 does.1
Like Chris, many students reason about fractions in ways that work in certain situations but not in others. Chris may have an image of a fraction as a quantity less than one–and as a whole with some pieces missing. His reasoning would be helpful if he were comparing the size of 4/6 and 5/6, but leads him to the wrong conclusion in the example above.
Students’ images of fractions are shaped by mathematics lessons and by real life experiences. What images of fractions do your students typically draw when asked to make sense of a fraction problem? The illustration below shows the fraction 3/4 shaded in eight different models.
Models of the Fraction 3/4
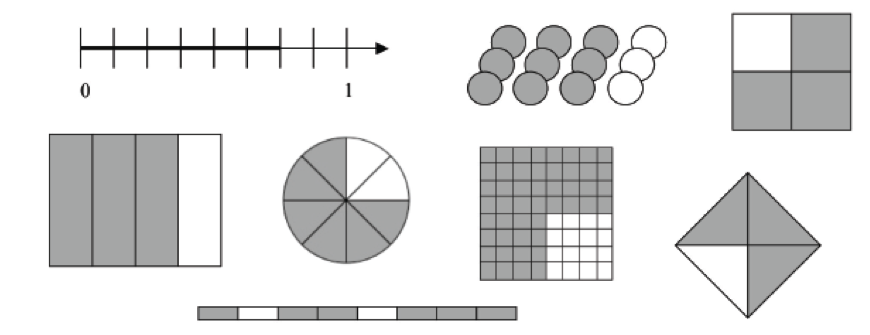
Each of the models above has different strengths and shortcomings for building student understanding. Tad Watanabe’s article "Initial Treatment of Fractions in Japanese Textbooks" argues that there is not one single “best” model, since ultimately students need to grasp that 3/4 represents several very different situations, such as 3/4 of a meter or 3 apples in a basket of 4 fruits. US textbooks rarely use a linear measurement context to introduce fractions, but it is common in other countries and in research-based programs, and it may help students see fractions as numbers that can go on a number line. In the next activity, you can experience fractions in a linear measurement context.
1 Adapted from Cramer, K. & Wyberg, T. (2007). When getting the right answer is not always enough: Connecting how students order fractions and estimate sums and differences. pp. 205-220. W. G. Martin & M. E. Strutchens (Eds.) The learning of mathematics. 69th Yearbook Reston, VA:NCTM, p.215.
Mystery Strip Activity
Create one strip of paper exactly 1 meter long and do not mark the strip in any way. See example below:

Then create the blue mystery strip by downloading the instructions from the resource tile below. Be particularly careful to follow the sizing instructions discussed in the document.
Do the Activity
- Put away rulers and other standard measuring devices!
- Without using standard measuring devices, express the length of the mystery piece as a fraction of a meter, for example: The mystery strip is ____ of a meter.
- Give team members time to try the problem individually and then discuss your approaches. It is an unfamiliar problem type, so you may find it useful to check out the solution approaches.
- What understandings of fractions help in solving this problem?
Solution Strategies
- What might they do to find the length of the mystery strip, using just the meter length?
- What if the mystery strip was 2/3 meter? How would they find the length?
- Can you use a similar process for your mystery strip?

