This course supports your team to conduct a Lesson Study cycle on fractions. Your team should include at least one grade 3-5 teacher who will be teaching a fractions unit.

Introduction
The tasks students do, and the sequence of these tasks over time, can dramatically shape how students imagine and think about fractions. To consider how students build their understanding of fractions based on their prior understanding of whole numbers, analyze the following two problems from a Japanese textbooks series and discuss the questions that follow the problems.
In grade 2, Japanese students investigate how many liters of water fit in various containers. (The shaded area represents the water.)

How many liters of water are there?
Then, in grade 3, Japanese students encounter the following related problem. (Assume that the 1-liter container is divided into equal parts.)
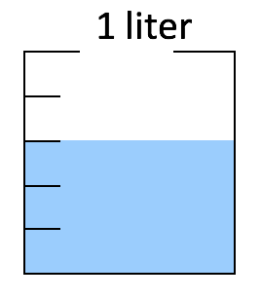
How much water is shown by each interval? How much water is in the container? How many liters are in the container?
Discuss:
- What are the similarities between the two problems shown above?
- What knowledge about whole numbers might students bring to the fraction problem?
- Some US students struggle to answer the question: “How many 1/5 are in 2/5?" How might the tasks above support their understanding?
What Images of Fractions Do Students Develop?
We examine a curriculum that introduces fractions using a linear measurement context and will see lesson videos based on the curriculum.
Read the grade 3 unit that introduces fractions in the Tokyo Shoseki curriculum (the most widely used Japanese textbook). It may be helpful to know that 8 periods of 45 minutes are allocated for this unit, roughly one period per textbook page.
Discuss:
How does this unit help students with the challenges explored in Module 1, such as to:
- See non-unit fractions (fractions with a numerator other than 1) as accumulations of unit fractions (fractions with numerator of 1)?
- See the connection between whole numbers and fractions?
- Connect area, linear measurement, and number line models?
How do the images and understandings of fractions that students might develop from this textbook compare with what students might develop from your own curriculum’s introduction of fractions?
Jot down: In Sections 3-5 of your Teaching-Learning Plan anything you want to remember for your own planning.
[insert here from pp. 21-top of 23 of green toolkit, view grade 3 video excerpts; edit as appropriate for web format]
Video of Lesson 1
Watch the video and take notes on the Video Observation Notes. To prepare, we suggest that you:
- Imagine how you would teach the beginning of the grade 3 fractions unit.
- Look over the Summary of Video Excerpts (Lesson Series 1) on page 26.
- Divide up the discussion questions below so that each team member focuses on one question, and note your focus question on a Video Observation Notes page. If your group meeting time is limited, members can watch the video on their own before your next meeting.
Use your Video Observation Notes to discuss the following questions. The Summary of Video Excerpts (Lesson Series 1) may also be useful in jogging your memory of the lesson.
- How does the instructor use the 1-meter reference strip? Why does he use two of the 1-meter reference strips to show 2 meters?
- Why does the instructor have students predict the length of pieces before investigating?
- What elements of instruction might help students build a strong mental image of the connection between the unit fraction and the whole: that 1/3 is a unit that goes into the whole 3 times, 1/4 is a unit that goes in 4 times, etc.?
- This veteran instructor made two changes from the strategies recommended by the Teacher’s Edition: He gave students strips representing just the fractional part over 1 meter (such as 1/3m), rather than the whole length (such as 1 1/3m), and he did not pre-draw lines on the 1-meter reference strip to show 1/3m, 1/2m, etc.). Why do you think he made these choices?
Video of Lesson 2
Watch the video and use your Video Observation Notes to discuss the following questions. The Summary of Video Excerpts (Lesson Series 1) may also be useful in jogging your memory of the lesson.
- The instructor takes considerable time to write on the board the different ways of expressing 1/4 meter. Do you think this is a good investment of time? Why or why not?
- Why do you think the instructor chose 2/5 m and 2/3 m as lengths for the mystery strips?
- The instructor chooses particular student misunderstandings as a focus for whole class discussion (for example, 2/3 m versus 2/5 m as descriptions of the mystery strip and two different lengths both thought to be 3/4 m.) What kinds of understanding do you think he was trying to build?
Video of Lesson 3
Watch the video and use your Video Observation Notes to discuss the following questions. The Summary of Video Excerpts (Lesson Series 1) may also be useful in jogging your memory of the lesson.
- How do students connect linear measurement activities to the number line?
- Why might it be useful to introduce fractions in the context of a standard linear measurement unit (meters) that is continuous? How might the students’ experience be different if fraction bars were used?
- How might these lessons build an understanding of the fractions standards in the Common Core (see Appendix C) or your state standards, especially:
- 3.NF.A.1: Understand a fraction 1/b is the quantity formed by 1 part when a whole is partitioned into b equal parts.
- 3.NF.A.2: Understand a fraction as a number on the number line; represent fractions on a number line diagram.
- 3.NF.A.3.D: Compare two fractions with the same numerator or the same denominator by reasoning about their size.
- 4.N.F.B.4.A: Understand a fraction a/b as a multiple of 1/b. For example, use a visual fraction model to represent 5/4 as the product of 5 x 1/4; recording the conclusion by the equation 5/4 = 5 x 1/4
