This course provides a structured, in-depth look at Teaching Through Problem-Solving, an approach that builds students’ mathematical knowledge, reasoning, and dispositions through problem-solving.

In this module, you will see how an experienced TTP practitioner plans and teaches a series of TTP lessons. Specifically, you will discover how the different instructional supports for a TTP lesson come together to build students’ understanding of a particular mathematical topic: area of polygons.
3.1 Examine the Content
To help students build the concepts in the mathematics curriculum– rather than be told those concepts –teachers need to know what their students currently know. Teachers also need to imagine how students might use their current knowledge to build the next mathematics in the curriculum. For these reasons, the first part of TTP lesson planning is investigating the curriculum content and students’ current understanding of it. When you do this in your own setting, you can draw on your own curriculum and standards.
Investigate Standards & Curriculum
Imagine that you want to plan a TTP lesson around the L-shape task below:
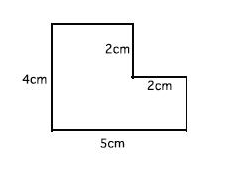
You first need to understand the unit context and larger mathematical trajectory into which this task fits. What role does this task play in building bigger mathematical ideas? What do students need to know to solve it? What are the important insights students might gain from solving this task?
Your Teacher’s Edition may explain the rationale for each task and how it relates to the unit and content trajectory. Or you may need to consult additional resources. In the case of this task, the Common Core State Standards and related Progressions for Geometry (especially pages 2-5 and p.16) and Geometric Measurement (especially pages 16-18) identify two important understandings that elementary students need to develop.
Composing and decomposing. Composing and decomposing figures provides an opportunity for students to learn about area as the “amount of two-dimensional surface that is contained within a plane figure” and to learn that “area is additive, i.e, the area of the union of two regions that overlap only at their boundaries is the sum of their areas” (CCSS progression geometry measurement K-5, 2012, p.4).
Spatial structuring. To measure area, students must mentally structure the space within a figure–for example, mentally structure a rectangle into rows and columns of square iterated units. The CCSS Progression for Geometry (p.4) notes that “Such spatial structuring precedes meaningful mathematical use of the structures, including multiplication and, later area….” and that “Early composition and decomposition of shape is a foundation for spatial structuring.” Students who are still developing an understanding of area may overlap or gap square units as they attempt to measure.
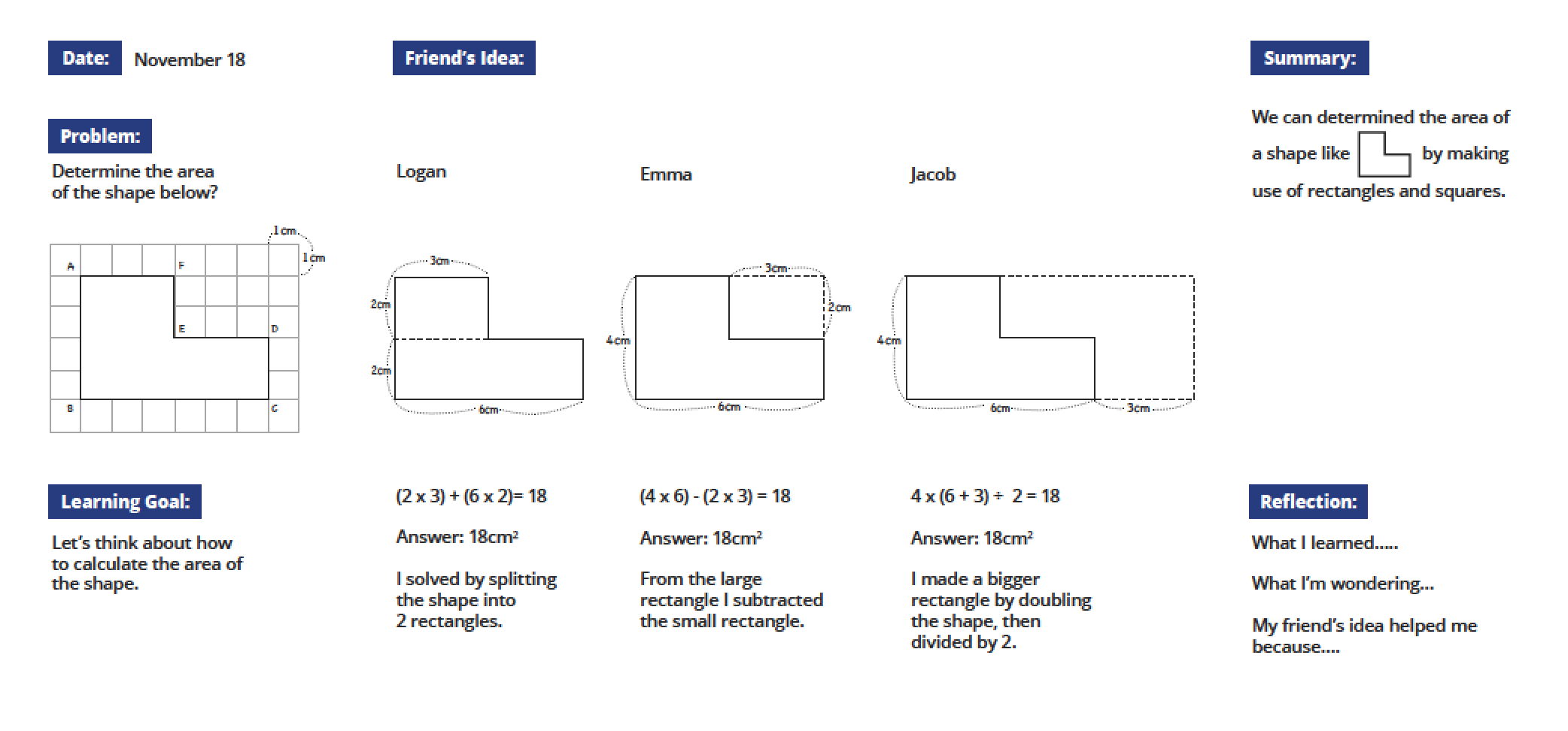
Below is a lesson plan developed by Dr.Takahashi that includes an explanation of the unit context and larger mathematical trajectory into which this task fits. Optional: Also included below is the video 'Can You Find the Area? (48 minutes). This video provides highlights from Dr. Takahashi's teaching of the three lessons described in the lesson plan. Segments of this video are used throughout the rest of this module.
Try the Problem and Anticipate Student Thinking
A next crucial step in planning a TTP lesson is to solve the lesson task and anticipate how students will solve it. Solve the tasks below and consider the following questions:
- How will students use what they already know to solve each problem?
- What will be common solution methods? What will be common mistakes and stumbling blocks? Why do these mistakes occur?
- What big mathematical ideas would we like students to learn by solving and discussing this task?
The two polygon area tasks shown below are well-suited to TTP. Depending on what students already understand, one or both tasks might be used within a unit plan. If students do not yet firmly grasp what area is, Problem 1 might be a good way to begin the unit. Once students understand rectangle area and its measurement, Problem 2 provides a good opportunity to see whether students can apply their knowledge to an L-shaped figure. So the first important step in planning a TTP lesson is understanding the unit goals, understanding what students know, and choosing the task that will help students take the crucial next step in their learning.
Problem 1
Which of the following shapes, the rectangle or the square, has the larger area, and by how much? Think about a way to express how large they are.
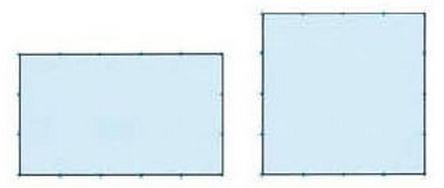
| Problem | What might this problem reveal about student-thinking? What kind of understanding might it build? |
| Compare the area of a square and rectangle (perimeter of 16; area of 16 & 15) |
|
Problem 2
Make the following shape on a geoboard (or dot paper) and find the area. (From “Can You Find the Area?” series of lessons on video by Akihiko Takahashi.)

| Problem | What might this problem reveal about student-thinking? What kind of understanding might it build? |
| Area of L-shape |
|
3.2 Board Organization
You can examine a sample board plan (below) for a lesson on the area of the L-shaped figure. It is not taken from Dr. Takahashi’s lesson series, but it may be useful in thinking through the student responses to expect and how they might be used to build students’ understanding of the lesson’s big ideas.
Click on image to expand view.
 Downloadable version available here.
Downloadable version available here.
Reflection Questions
- What do you notice about the learning goal written on the board for this lesson?
- How does the organization of student ideas on the board build mathematical understanding?
- How might consistent organization of the board benefit your students?
3.3 Teacher Questioning
Now that we have studied the mathematical content and reviewed the instructional plan, let’s view video segments from the series of three lessons “Can You Find the Area?” taught by Dr. Akihiko Takahashi. The video can help us consider teacher questioning strategies to elicit, support, and advance student thinking. Since Dr. Takahashi is a guest teacher who is not teaching his own students, he begins with a task that allows him to gauge what students know about area, and to build common understandings within the class.
In the first lesson, Dr. Takahashi begins by asking students to make a 4 X 5 rectangle on a geoboard and to copy the shape onto paper (dotted to look like a geoboard). Before watching this video segment, discuss or reflect on:
- What important misunderstanding(s) might this task reveal, and how might you handle the misunderstanding(s)?
Students may be accustomed to listening carefully to the teacher, but not to fellow students. So it may take some careful development of students’ presentation skills and listening habits to build lessons in which students use each other’s thinking as an important resource for development of mathematical ideas.
Watch Video Segment 1 and note down the questions and moves used by Dr. Takahashi to help students:
- Present their solutions in a way that is visible and audible
- Explain their thinking
- Understand and value classmates’ thinking
- Compare ways of thinking
Discuss what you noticed and keep a record of any strategies you want to remember for your own teaching through problem-solving.
Video Segment 1
In the next video segment, Dr. Takahashi poses the problem of finding the area of the L-shaped figure below:

Students work on the problem independently, and then Dr. T. orchestrates a discussion in which selected students share and explain their solutions to classmates. Watch Video Segment 2 and note down:
- The questions and moves by the teacher designed to help students present, explain, attend to and understand each other’s thinking
- The features of materials design and blackboard use that help students grasp each other’s solution methods
- The features that help students connect visual and verbal representations with mathematical expressions
Consider anything new you noticed about the above points, and record any teacher moves or teacher questions you want to remember for your own teaching through problem-solving.
Video Segment 2
3.4 Neriage (“Kneading”) Discussion
The next video segment (which immediately follows the prior segment of the lesson) shows the final portion of the lesson, in which students look back on what they learned that day and summarize key mathematical points. The neriage, in which students compare solution methods and draw out key mathematical points, has begun in the previous segment and is revisited and summarized in this segment. Before watching video segment 3, examine the student responses (below) and discuss with your team:
- What mathematical ideas has Dr. Takahashi emphasized in the discussion of the solutions so far?
- What do you expect him to emphasize in the summary of the lesson?
- What questions do you expect Dr. T. to ask?
Watch Video Segment 3 and make note of
- The mathematical ideas emphasized
- Teacher questioning and moves to elicit the mathematical ideas
Video Segment 3
Lesson Summary
To summarize a lesson focused on finding the area of an L-shaped figure, Dr. Takahashi drew out the ideas that:
- The L-shape can be split up in different ways, yielding different mathematical expressions, but these different solution methods yield the same total area;
- The L-shape can also be seen as part of a larger rectangle, so that rectangular areas can be subtracted to find the total area.
- Addition and multiplication can both be used to find the rectangle area, but the more efficient strategy of multiplication cannot be used for the L-shape without first decomposing (or composing) rectangles.
In the next lesson, Dr. Takahashi asks students to find the area of the shape shown below using what they learned in the prior lesson.
Watch video segment 5 (below) and consider why Akihiko Takahashi chose these four student solutions (below) to be shared on the board, and note the important mathematical points to be elicited.
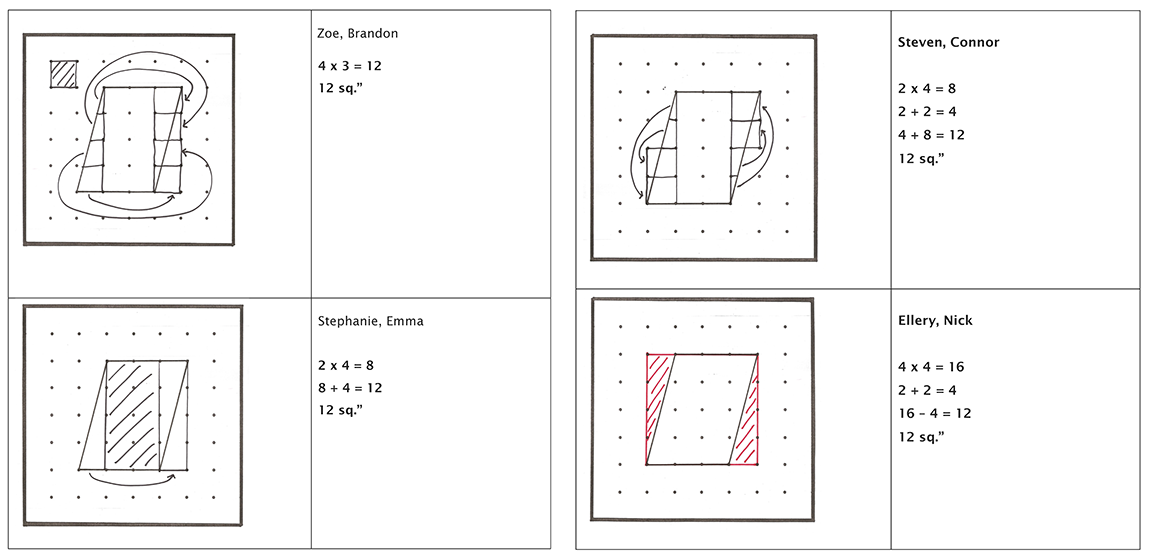
Video Segment 5
3.5: Reflective Student Journals
Watching segments from the video “Can You Find the Area?”(see Video Segment 4 and Video Segment 6) may also spark your thinking about how to build students’ journal writing habits. At the end of each of three consecutive lessons, Dr. Takahashi asks students to write about what they learned, and he selects several journals to be copied and read aloud at the beginning of the next lesson. He deliberately selects journals that model features he would like students to incorporate (such as drawings, mathematical expressions, and comparison of solutions). As you watch the video, consider different functions of journals, such as helping students:
- Recall key ideas from the previous lesson to be carried forward into the current lesson;
- See the value of one another’s ideas;
- Organize and revisit their own thinking;
- Reflect on how and why their thinking changed.
Video Segment 4
At the beginning of lesson 2, students read their written reflections sharing what they learned about finding the area of the L-shape.
Video Segment 6
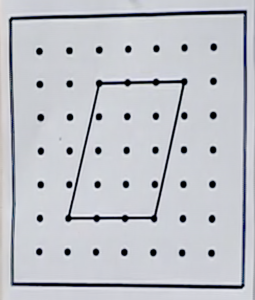
At the beginning of lesson 3, students read their written reflections sharing what they learned about finding the area of a parallelogram.



