To enable students to build the new mathematical ideas, four instructional routines are especially important in TTP classrooms:

• board organization
• student reflective journals
• teacher questioning
• neriage (“kneading”) discussion

In this section, you will investigate the basics of each of these instructional routines, and learn about how they foster student learning.

2.1: Board Organization

A well-organized board can help students by creating a public record of the lesson so that students can:

• Revisit each element of the lesson as needed–for example, refer back to the problem, related prior knowledge, a key model or illustration, etc.
• Compare different solution strategies and consider how their own thinking relates
• See the mathematical expression, visual model and verbal description associated with each solution strategy
• Experience an organized model for their own note-taking and reflection
• Become “meta-cognitive” as they see how new ideas are developed in mathematics

Board organization supports equity, by keeping information available to students who need extra time to read or integrate information. Likewise, students who are momentarily distracted can revisit the lesson’s ideas and re-enter the lesson.

In Japan, board writing often seems spontaneous, because it features ideas and student work that emerge during the lesson. In fact, teachers typically plan board writing in advance of the lesson, by thinking about the key ideas and pictures on the board that will spark, capture and advance students’ thinking. International comparisons reveal that Japanese mathematics teachers use the board more frequently than do teachers in Germany and the U.S., and that Japanese teachers tend to keep the board writing throughout the lesson, rather than erasing parts of it during the lesson. The board writing provides a record of the lesson that students can consult as they summarize and reflect on what they learned.

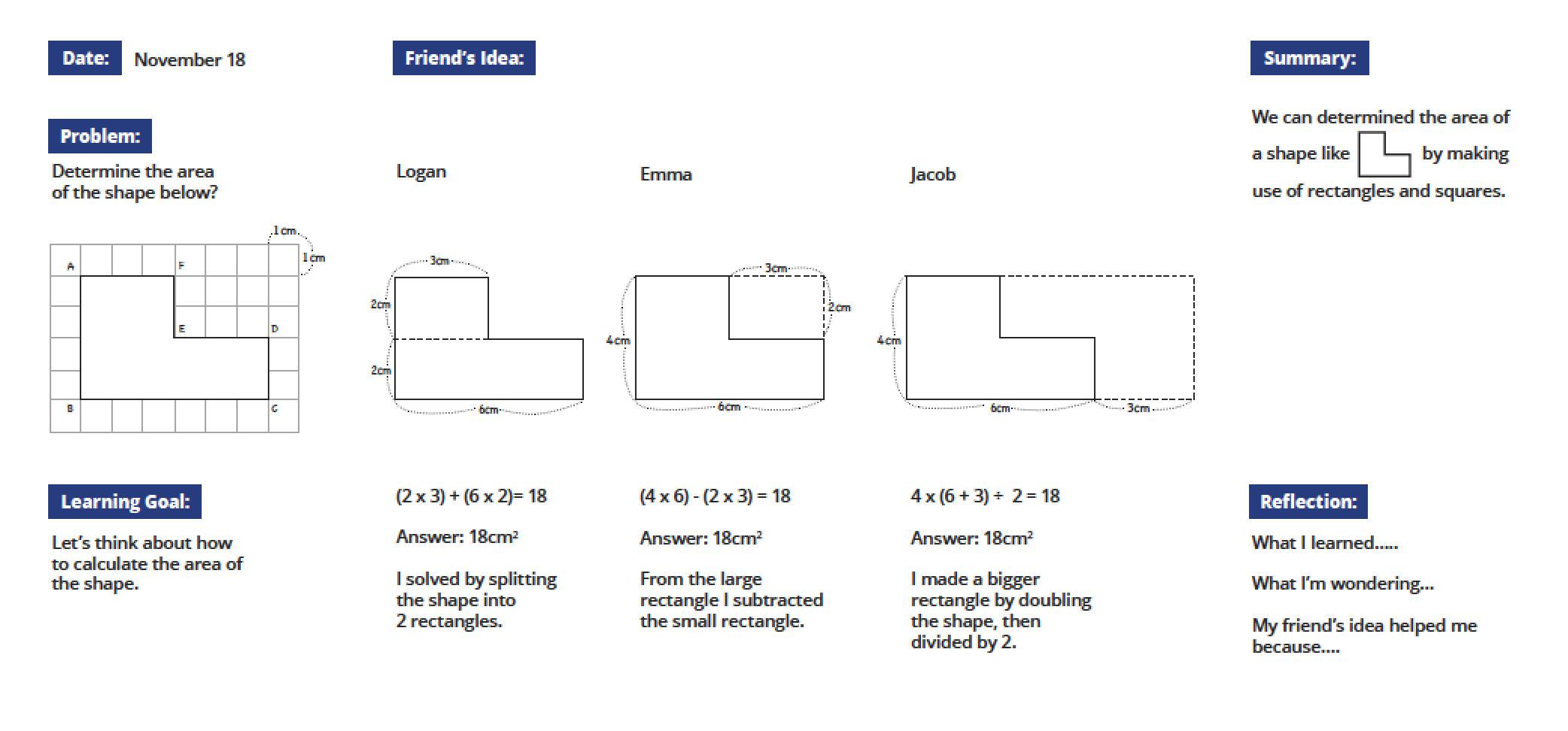
Creating a board plan also can help teachers by providing an opportunity to think through the whole lesson--from posing the problem, to student work that will be shared, to the key ideas that will emerge from the neriage discussion. A sample board is shown below.

Click on image to expand view.

Downloadable version available here.

• The problem posed to students is shown at the upper left of the board, so students can refer back to it.
• The “learning goal” captures the problem as we hope students will pose it themselves.
• The “friend’s idea” section of the blackboard captures student thinking and the student solution methods you select for presentation, in the order you want to discuss them, along with key information such as visual and mathematical models.
• The “summary” includes the mathematical points you hope to draw out of neriage (“kneading”) discussion.

Smartboard users can consider how to use their chosen technology to provide similar supports for students to actively build the new mathematical ideas.  The video excerpts from Akihiko Takahashi’s lesson Ways of Counting and Mathematical Expression and Joshua Lerner’s lesson Conceptual Understanding of Multiplication provide some ideas for smartboard users. Play the videos below to see their lessons; the dots underneath each video allow you to scroll through each series of 4 lessons.

Ways of Counting and Mathematical Expression

Conceptual Understanding of Multiplication

Reflection Questions

1. How is the board organization for TTP similar to or different from what you currently do?
2. What, if anything, is puzzling?
3. How do you think board organization used throughout the year might support struggling learners?

2.2: Student Reflective Journals

Reflective journals provide a place for students to copy (or paste) and solve the problem, record classmates’ ideas, and update their own thinking over the course of the lesson, based on discussion of classmates’ ideas. At the end of the lesson, students write reflections that capture what they learned–about the problem-solving process as well as the mathematical content. Journals thus provide a place for students consolidate their mathematical knowledge and to reflect on the evolution of their own thinking–to become metacognitive.

Journals also support students to:

• Revisit what they have learned in previous lessons;
• See the growth in their own mathematical practices and knowledge;
• See the value of each other’s ideas;
• Reflect on how and why their thinking changed.

Click on image to expand view.

Adapted from Mathematics 4B for Elementary School, H. Hironaka & Y. Sugiyama (eds.), 2006, Tokyo: Tokyo Shoseki Ltd. Copyright 2006 by Tokyo Shoseki Ltd. Adapted with permission.

The key elements in a journal entry are

• Date
• Problem: a verbatim copy of the problem to be solved during the lesson
• My Idea: any number sentences, models, representations, or other information that the student generates during independent think-time or as the lesson continues
• My Friend’s Idea: a copy of the strategy shared by one of the students during the whole-class discussion
• Summary: a summary of the major learning in the lesson; typically, this is generated collaboratively by the class
• Reflection: students write 1-2 sentences summarizing what they learned; how their ideas changed; their wonderings and questions; how they are feeling, etc.

A TTP lesson usually begins by reading aloud several students’ journal reflections from the prior day that were selected by the teacher. (These may be printed so students can paste them in their journals). These journal entries are selected to highlight knowledge to be carried forward from the prior day’s lesson and mathematical practices the teacher would like to encourage–such as writing mathematical expressions, recognizing the merits of classmates’ solutions, reflecting on mistakes, or posing a question.

Watch two video excerpts to find out more about how teachers use math journals in the classroom.

Reflection Questions

1. How is the use of reflective journals in TTP similar or different to practices in your current instruction?
2. How do you think reflective mathematics journals might benefit your students?
3. What seems challenging about reflective mathematics journals?

2.3: Discussion

Visitors to Teaching Through Problem-solving lessons often remark on the quality of student-led discussions. As one visitor commented, “The students ask ‘teacher questions.'” After presenting their work at the board, students call on classmates for comments and questions. Watch an example of this routine in the video below.

How do students learn to have powerful discussions?  Two important building blocks are:

• Teacher questioning
• Speaking and listening routines

Teacher Questioning

The teacher’s questioning provides a model of the questions that we hope students will internalize and will learn to ask on their own. Click on the flowchart below to see examples of teacher questions during each phase of a TTP lesson, and to consider the purpose of questioning during each phase.

Neriage ("Kneading") Discussion

Perhaps the most difficult aspect of a problem-solving lesson is “neriage” (pronounced nary-ah-gay) – a Japanese term for “kneading” or “polishing” students’ ideas through discussion. As shown in the figure “Beyond Show and Tell,” neriage occurs after students come up with ideas to solve the problem. The point of a problem-solving lesson is not simply to solve the problem; it is to develop important mathematical ideas. Neriage builds a bridge from students’ current solution methods to these mathematical ideas.

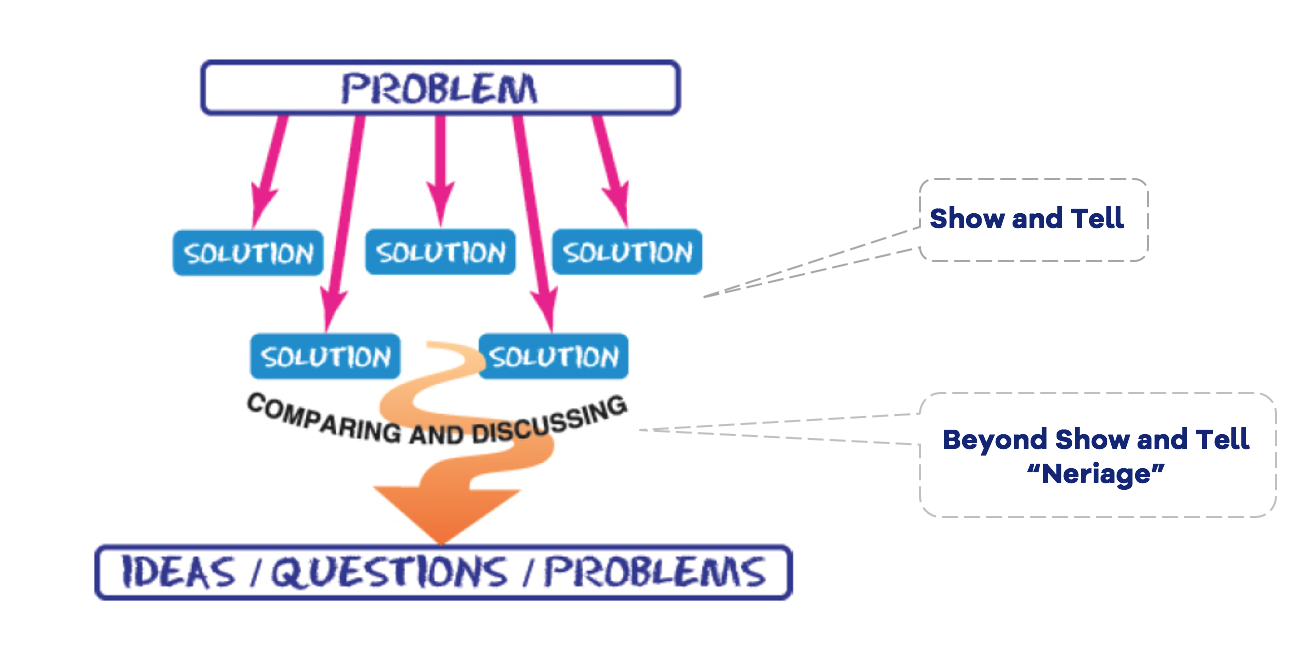
from Teaching Mathematics Through Problem-solving by Tom McDougal and Akihiko Takahashi (2014) 

Planning the neriage will support you in identifying the big ideas(s) you want students to take away from the lesson and the summary you hope the lesson will produce. As the summary emerges at the end of the lesson, writing it on the board helps students consolidate their thinking and write it in their notes to later revisit if needed. Drawing the summary from students’ own comments and work is especially powerful.

Reflection Questions

1. How is your current questioning similar to that outlined for TTP, both in purpose and content? How is it different?
2. To help your students actively question and make sense of each other’s solutions, what classroom routine(s) would you like to build in your classroom? How will you do that?
3. Is your current discussion model more like “show and tell” or more like neriage? What do you see as the value of going beyond “show and tell” to whole-class neriage discussion?

For more information, consider reading:

• Beyond Show and Tell for Teaching Through Problem-solving by Dr. Akihiko Takahashi