Overview

In this resource, we discuss the first situation types that students typically experience when introduced to addition and subtraction story problems in Kindergarten. Studying these situations allows teachers to see how students begin to understand the fundamentals of addition and subtraction.

This resource builds on some of the concepts and frameworks first introduced in our overview resource, Addition and Subtraction, Part 1: Story Problems.

Key Concepts

In addition to providing a closer look at the add-to, take-from, and put-together/take-apart situations, this resource focuses on two key concepts associated with these initial situation types:

• Add-to and take-from situations represent a sequence of events which involve one quantity turning into a new quantity, while put-together/take-apart situations represent a shift of perspective: you must be able to see two quantities as one combined quantity, or vice-versa.
• Emphasizing action when representing story problems helps students generalize the relationships among quantities in each situation type.

Add-to and Take-from Situations

Add-to

In our first resource in this series, we took a close look at the add-to situation. As a quick recap: in this situation, the start quantity is always increased by the change quantity, giving us the result quantity. We represent the situation with an example problem and diagram below. We do not recommend using the diagram as a model for students, but hope it may be helpful to understand the situation type as teachers.

In this example, as is typically the case with introductory add-to problems, the result quantity is unknown. The result is the easiest quantity to solve for in this situation, making this type of problem the typical entry point for addition story problems.

Take-from

The take-from situation is quite similar to the add-to situation (including how the quantities are named), but has one important difference. Instead of increasing the start by the change, we decrease the start by change (i.e. take the change away) to give us the result. This is represented below.

As with the add-to situation, the take-from situation is typically introduced with asking students to solve for an unknown result quantity. This type of problem also serves as the typical introduction to subtraction in Kindergarten.

REFLECT — Take a few minutes to reflect on the following questions individually or as a team.

• What kind of problems do you start with when you introduce addition to students? What about subtraction?

Put-together/Take-apart Situations

Put-together

The other situation that often informs students’ initial understanding of addition is put-together. An example of a put-together problem and a diagram representing the situation type follows.

In a put-together situation, there are two separate quantities that are both referred to as addends in the CCSS (in our example, 3 goldfish and 2 goldfish). Then, when these two quantities are considered altogether, they become a new, single quantity, called total (in this case, 5 goldfish). Thus, in a put-together situation, we are changing the way we see those two quantities.

Put-together situations always involve solving for an unknown total.

Take-apart

Parallel to the put-together situation is another situation students typically encounter in their early study of subtraction: the take-apart situation. In the put-together situation, we solved for the unknown total, but in the take-apart situation we solve for an unknown addend. We show this below.

As we see in the example problem above, in the take-apart situation we solve for a missing addend (the number of white rabbits) given the total (8 rabbits) and the other addend (5 grey rabbits).

A Closer Look at Put-together/Take-apart Situations

Now that we have an understanding of the situations students tackle in Kindergarten, it’s worth examining some subtle but important characteristics of the put-together/take-apart situations.

Two Sides to the Same Coin

You may have noticed that add-to and take-from situations are quite similar.  We compare the two in the chart below.

In the Cognitively Guided Instruction (CGI) research, both put-together and take-apart situations are considered as part-part-whole situations. Put-together situations are part-part-whole situations when the whole is unknown, and take-apart situations are those in which a part is unknown. It can be useful to think of these situations together as part-part-whole situations, because it helps us see that addition is called for when the whole is unknown, and subtraction is called for when a part is unknown.

Put-together and Take-apart Situations are Static

Add-to and take-from situations represent a sequence of events. For example, “There are 8 rabbits and 3 rabbits leave. How many bunnies remain?” Because students have an easy time understanding this sequence, add-to and take-from situations (when solving for an unknown result) can often be very intuitive.

In contrast, put-together and take-apart situations are static: all the quantities are present at the same time. In our example above, a student is asked to see white rabbits, grey rabbits, and also a combined set of grey and white rabbits. This requires more flexible thinking from the student.

In general, the static nature of put-together and take-apart situations cause them to be more abstract than the sequence of events in add-to and take-from situations—and they may be more difficult for students to understand in their initial studies of addition and subtraction.

REFLECT–Take a few minutes to reflect on the following questions individually or as a team.

• If you were a Kindergartener how would you model the following take-from and take-apart problems with manipulatives?
  • There are 8 rabbits and 3 rabbits leave. How many bunnies remain?
  • There are 8 rabbits. 3 of them are white. How many are grey?
• Which problem was easier to model? Why?

Showing Action in Situations

You may have noticed a hand pushing away blocks in each textbook example problem shown above. It is common for Japanese curricula to emphasize this type of action in story problems because it helps students generalize what is happening in each situation. For example, in add-to situations, students come to realize that although the details of the story problems may differ, one quantity (the change) always joins an existing quantity (the start), and that this can always be represented by pushing one quantity towards another, as shown with the blocks below.

This action (which is how students often model the problem type) can be made visible on the board by using arrows as we illustrate below.

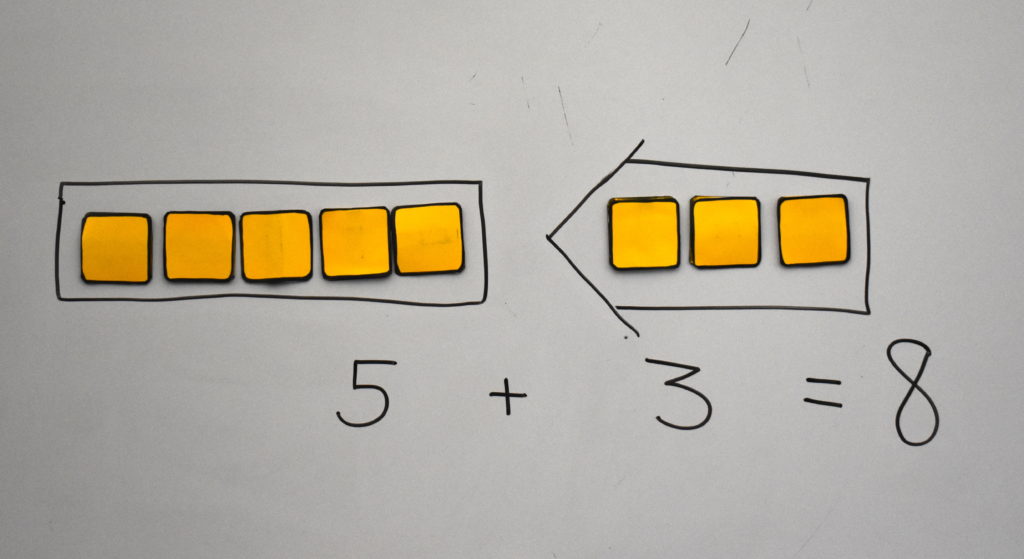
Below, we show the textbook and board action representations for each of the initial situations students learn.

You may notice that action is associated even with the static situations. The rabbits are not moving in the take-apart problem, so why are we pushing blocks away? Although no quantity is actually removed in this situation, it can help students to visualize taking away the known addend (the white rabbits) from the total (8 rabbits in all) to find the missing addend (the number of grey rabbits). This helps students reason that the operation to find the missing part is subtraction.

Discussion Questions

1. What ideas about the initial teaching-learning of addition and subtraction discussed in this resource strike you as important in your setting?
2. How does your curriculum handle initial addition and subtraction story problems? What about it do you like and/or notice that has opportunity for improvement?
3. What experiences have your students had that currently inform their understandings of add-to, take-from, and put-together/take-apart situations?
4. How do you and your students represent addition and subtraction problems on the board?
5. What do you want to learn more about and what steps can you take to do so?

Next Steps

In our next resource, we will continue discussing the teaching and learning of addition and subtraction by showing how students develop their understanding of the “compare” situation.

Use the links below to continue, or to review the other steps in the sequence.