Teaching Through Problem-solving
In Teaching Through Problem-solving (TTP), students develop each new mathematical concept by solving a problem that illuminates it.
The key to effective boardwork is doing the problem yourself and then anticipating how your students will solve it. It is from this perspective you monitor, select, and sequence the student work to share on the board.
—Alex Johansen-Laughlin
Prieto Math and Science Academy, Chicago
Board Organization
- Revisit each element of the lesson as needed–the problem, a key model or illustration, classmates’ solution strategies, etc.
- See the “story” of the lesson, from the initial problem, through the solutions and insights developed by the class, to the summary of what they learned
- Compare different solution strategies and consider how their own thinking relates
- See the mathematical expression, visual model and verbal description associated with each solution strategy
- Experience an organized model for their own note-taking and reflection
- Become “meta-cognitive” as they see how new ideas are developed in mathematics
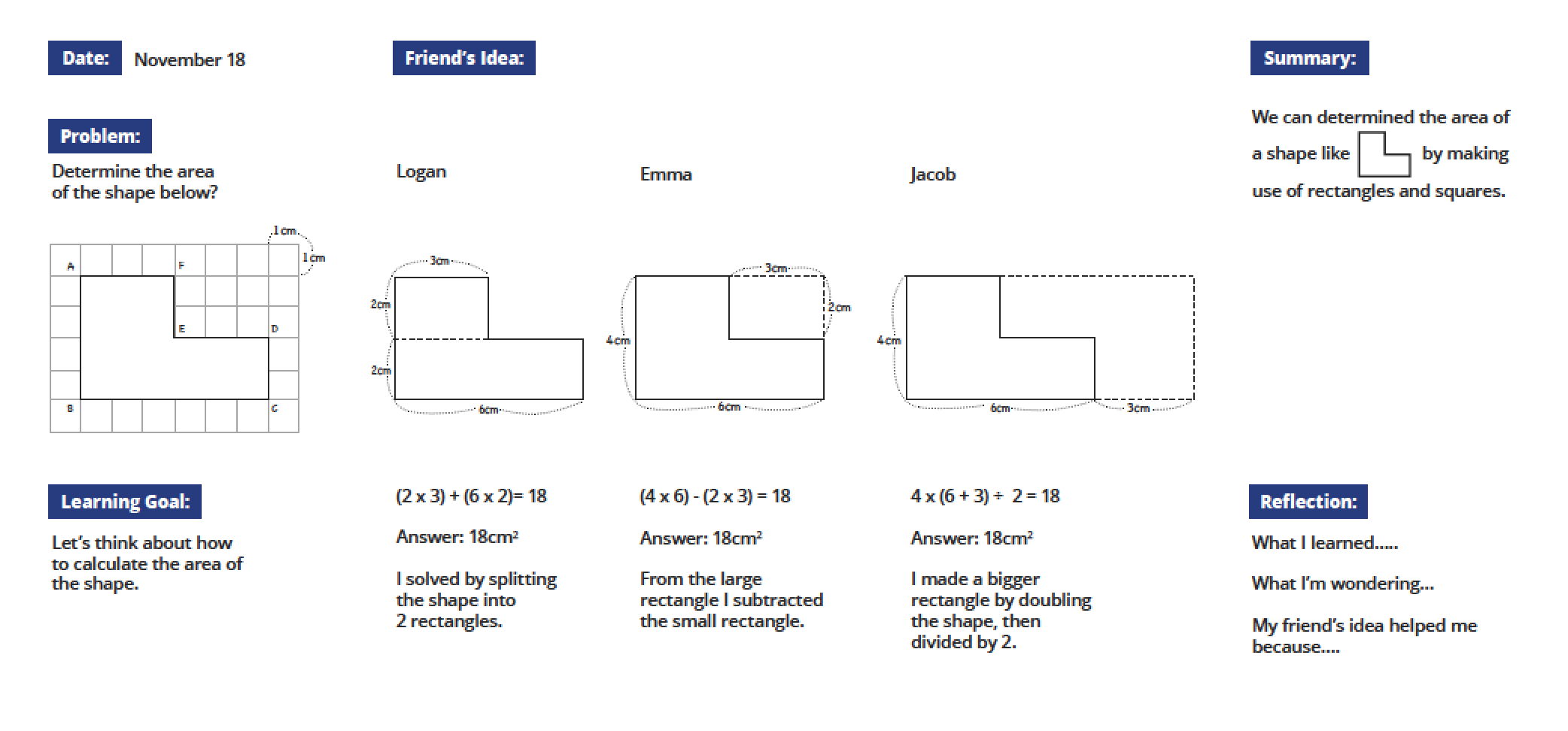
Sample Board
Notice the features of the sample board below, and imagine how consistent organization of the board in this way might benefit your students.
- The problem posed to students is shown at the upper left of the board, so students can refer back to it.
- The “learning goal” captures the problem as we hope students will pose it themselves.
- The “ friend’s idea” section of the blackboard captures student thinking and the student solution methods you select for presentation, in the order you want to discuss them, along with key information such as visual and mathematical models.
- The “summary” includes the mathematical points you hope to draw out of neriage (“kneading”) discussion.
Japanese board writing often seems spontaneous, since it features ideas and student work that emerge during the lesson. In fact, teachers typically plan board writing in advance, as they think about the key ideas and models on the board that will spark, capture and advance students’ thinking.
International comparisons reveal that Japanese mathematics teachers use the board more frequently than do teachers in Germany and the U.S., and that Japanese teachers tend to keep the board writing throughout the lesson, rather than erasing parts of it during the lesson. The board writing provides a record of the lesson that students can consult as they summarize and reflect on what they learned.
Teachers often find that creating a board plan provides an opportunity to think through the whole lesson–from posing the problem, to choosing and sequencing student work that will be shared, to identifying the key ideas that will emerge from the neriage discussion and the summary.
Smartboard users can consider how to use their chosen technology to provide similar supports for students to actively build the new mathematical ideas. Video clips from Akihiko Takahashi’s lesson Ways of Counting and Mathematical Expression and Joshua Lerner’s lesson Conceptual Understanding of Multiplication provide some ideas for smartboard users.
