Teaching Through Problem-solving

In Teaching Through Problem-solving (TTP), students develop each new mathematical concept by solving a problem that illuminates it.

An elementary-age male student points while his female teacher stands beside him and observes

The teacher should never say anything that a student could say.
—Akihiko Takahashi

Associate Professor of Elementary Mathematics, DePaul University, Chicago, IL

Speaking and Listening Routines

Visitors to Teaching Through Problem-solving lessons often remark on the quality of student-led discussions. As one educator who visited a public research lesson commented, “The students ask ‘teacher questions.’” Typically, students expect to field questions from classmates after they present their work at the board; you can see examples of this routine in the video below.
Routines for presenting and discussing work are built beginning in Kindergarten, when teachers help students speak in a loud voice, use hand signals to show their responses, and formulate questions for the presenter. Video from Prieto Mathematics and Science Academy (a Chicago public school) captures presentation and discussion routines at different grade levels, along with teachers’ reflections on how they built these routines.

Teacher Questioning

Download

A second powerful influence on student-led discussion is the questions that teachers ask, which provide a model for the questions that we hope students will internalize and will learn to ask on their own. Click on the arrows below to see examples of teacher questions during each phase of a TTP lesson and the purpose of questioning during each phase.

PURPOSE OF TEACHER QUESTIONING

Encourages students to:

  • want to solve the problem
  • notice what is similar or different from prior problems they have solved
  • notice what is similar or different from prior problems they have solved

EXAMPLES OF TEACHER QUESTIONS

  • What is the problem asking?
  • What do we know that might help us solve this problem?

PURPOSE OF TEACHER QUESTIONING

Encourages students to:

  • try to use what they know
  • try to solve the problem using important reasoning tools (mathematical expressions, models, etc.)
  • try to solve the problem using important reasoning tools (mathematical expressions, models, etc.)

EXAMPLES OF TEACHER QUESTIONS

  • What do you know?
  • What do the numbers in the problem mean?
  • How do the numbers in the problem show up in your picture?
  • How can you convince others?
  • Can you write a mathematical expression for your method?
  • Can you write a mathematical expression for your method?

PURPOSE OF TEACHER QUESTIONING

Encourages students to:

  • understand classmates’ ideas and compare and connect them
  • consider the accuracy, efficiency, and generalizability of presented ideas
  • connect their own ideas with presented ideas

EXAMPLES OF TEACHER QUESTIONS

  • How many solved it this way?
  • Can you explain what Shavon did?
  • Do you agree with this method?
  • What is the same and different about Sam’s and Marika’s methods?
  • What are the good points and difficulties of each solution method?
  • Are there any more ways to solve this?
  • Will this always be true?

PURPOSE OF TEACHER QUESTIONING

Encourages students to:

  • summarize what they learned
  • individually write about their own learning after hearing classmates’ summaries

EXAMPLES OF TEACHER QUESTIONS

  • What did we learn today?
  • How did my ideas change?
  • What method used by a classmate do I want to try?
  • What do I wonder about?
The New Learning is what students actually take away from the lesson, as reflected in their journal writing, their work and ideas during class, and the exit task, if any. Identifying what students took away, and noticing any ideas that are fragile or partial, allows teachers to develop questions for the next lesson.

Students will internalize questioning only if they find it useful. The next section explores how to plan a discussion in which students’ presentations and questioning build the new mathematics of the lesson. When students experience insights and build new mathematical concepts through discussion of classmates’ work, they will be hooked on the power of questioning.

Neriage Discussion

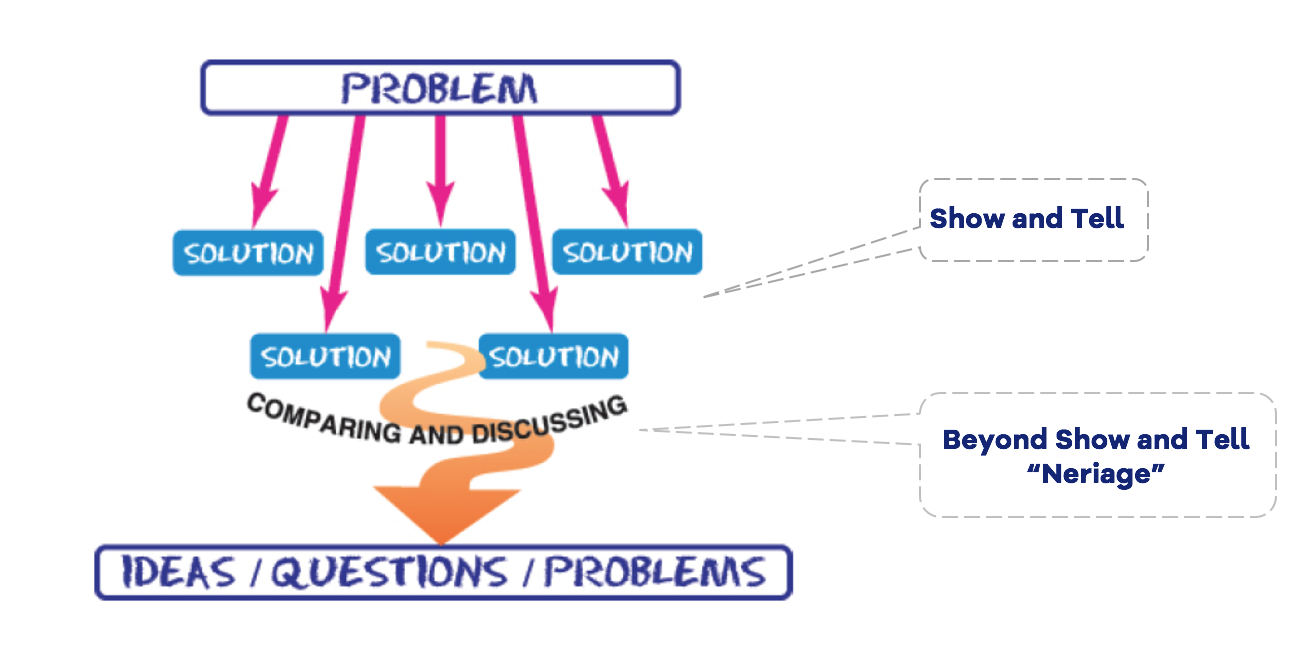
Perhaps the most difficult aspect of a problem-solving lesson is neriage (pronounced nary-ah-gay) – a Japanese term for “kneading” or “polishing” students’ ideas through discussion. As shown in the figure below, neriage occurs after students come up with solutions to the problem. The point of a problem-solving lesson is not simply to solve the problem; it is to develop important new mathematical ideas through neriage that helps students build a bridge from their current solution methods to these mathematical ideas.
Neriage provides the bridge from students’ current understanding to the new concept or procedure you want them to understand by the end of the lesson. (This understanding may be fragile at first, to be strengthened through future use.) Questions to help you plan the neriage are:
  • What knowledge will students bring to the problem?
  • What new understanding will they build during the lesson? (What actions or words will show their new understanding?)
  • What experiences and insights will help students progress from their initial knowledge to the new understanding? For example, what do you expect students to learn from the task itself and from comparing different solution approaches?
  • What specific features of different solution approaches will be important for students to notice? What questions will help students notice them?

Summary and Reflection

Following the neriage discussion, be sure to save time (at least 5 minutes) for the class to generate a lesson Summary, followed by time for students to write individually in their math journals about what they learned. The Summary can be initiated with a question like “What did we learn as a class today?” followed by sharing ideas. As you plan the neriage, you should have developed a clear statement of the summary you hope will emerge from the lesson, but it is powerful to use students’ own language to create the Summary on the board. If students do not summarize their learning in the way you hoped, this is powerful (if disappointing!) feedback for you.

By copying the Summary from the board into their math journals, students may be able to solidify their thinking; they also create a record of their learning from each lesson that can provide a valuable future reference.  After students have written the Summary in their notes, they can immediately go on to write their Reflections, which highlight their own personal learning from the lesson. The Journals tab provides further information on nurturing student Reflections and using them to introduce each TTP lesson.

Can’t find a resource you need? Get in touch.

Contact Us
Menu